지난번에는 타원곡선에 대해서 알아보았다. 이번에는 유한체의 타원곡선에 대해서 알아보자.

유한체는 유한개의 원소를 가지는 체(Field)이다. 체는 원소들 간의 덧셈, 곱셈의 연산 결과가 다시 그 안에 있는 (닫힘성)을 갖는 대수적 구조이다. 다시 말해 유한체는

  • 유한개의 원소들이 집합을 이루면서,
  • 덧셈과 곱셈 연산 두 쌍을 자유롭게 사용할 수 있고, (2개 연산자 사용)
  • 각 원소가 0이 아닌 원소로 나눌 수 있는 대수적 구조 (곱셈 역원 존재)

이다.

유한체에서의 타원곡선을 그려 보자. 다음 타원 곡선을 그려보려고 한다. \(y^2 = x^3 + 7\)

# 타원 곡선을 정의하자. 유한체에서 타원곡선을 정의하기 위해 prime 으로 modular 연산을 하자.
prime = 53
def ecc(x):
    return (x**3 + 7) % prime

# 53x53 범위 내에서 주어진 식을 만족하는 점을 모두 찍어보자.
points = []
for x in range(prime):
    for y in range(prime):
        if ecc(x) == (y**2)%prime:
            points.append((FieldElement(x, prime), FieldElement(y, prime)))
            
fig = plt.figure()
plt.xlim(0, prime)
plt.ylim(0, prime)

for (x, y) in points:
    plt.scatter(x.num, y.num, s=10, c='b', alpha=0.1)
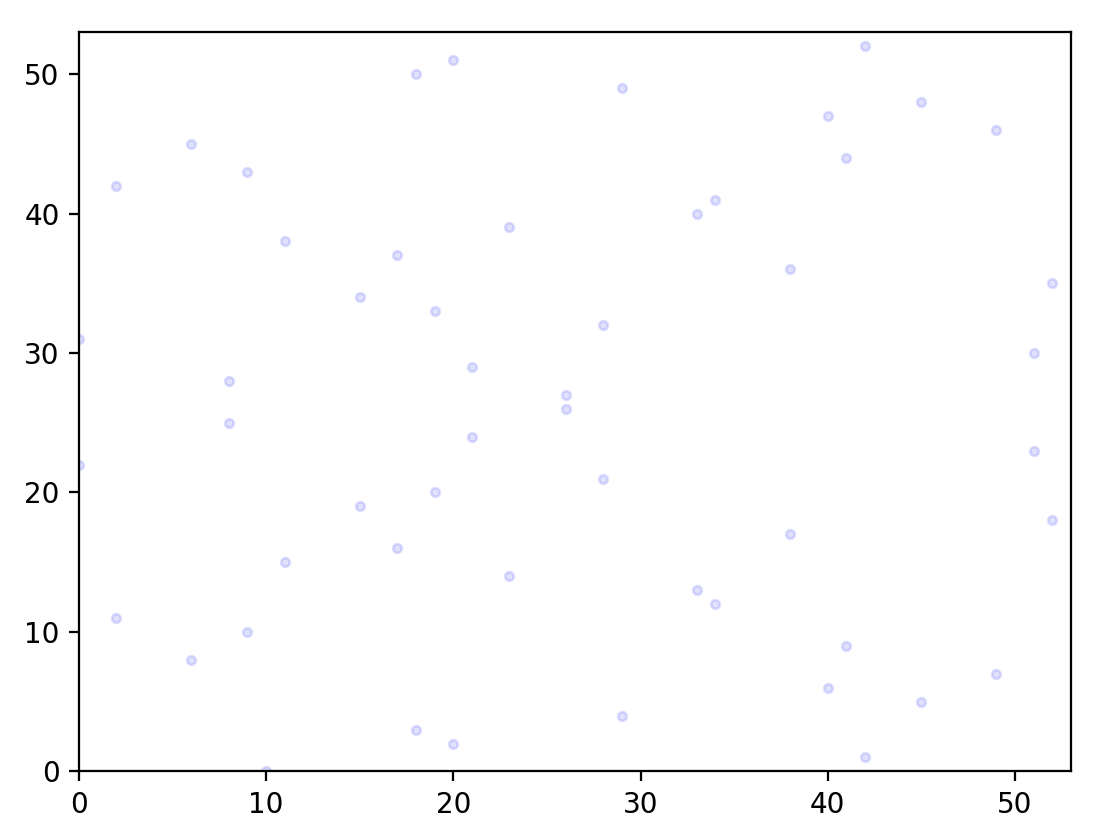
views
유한체의 타원곡선

유한체이기 때문에 곡선이 아닌 점들의 집합으로 나타낸다. 점만으로는 원래의 타원곡선 형태를 알기 어렵다.

Elliptic Curves over Finite Fields 에서도 동일한 그래프를 그려 볼 수 있다.

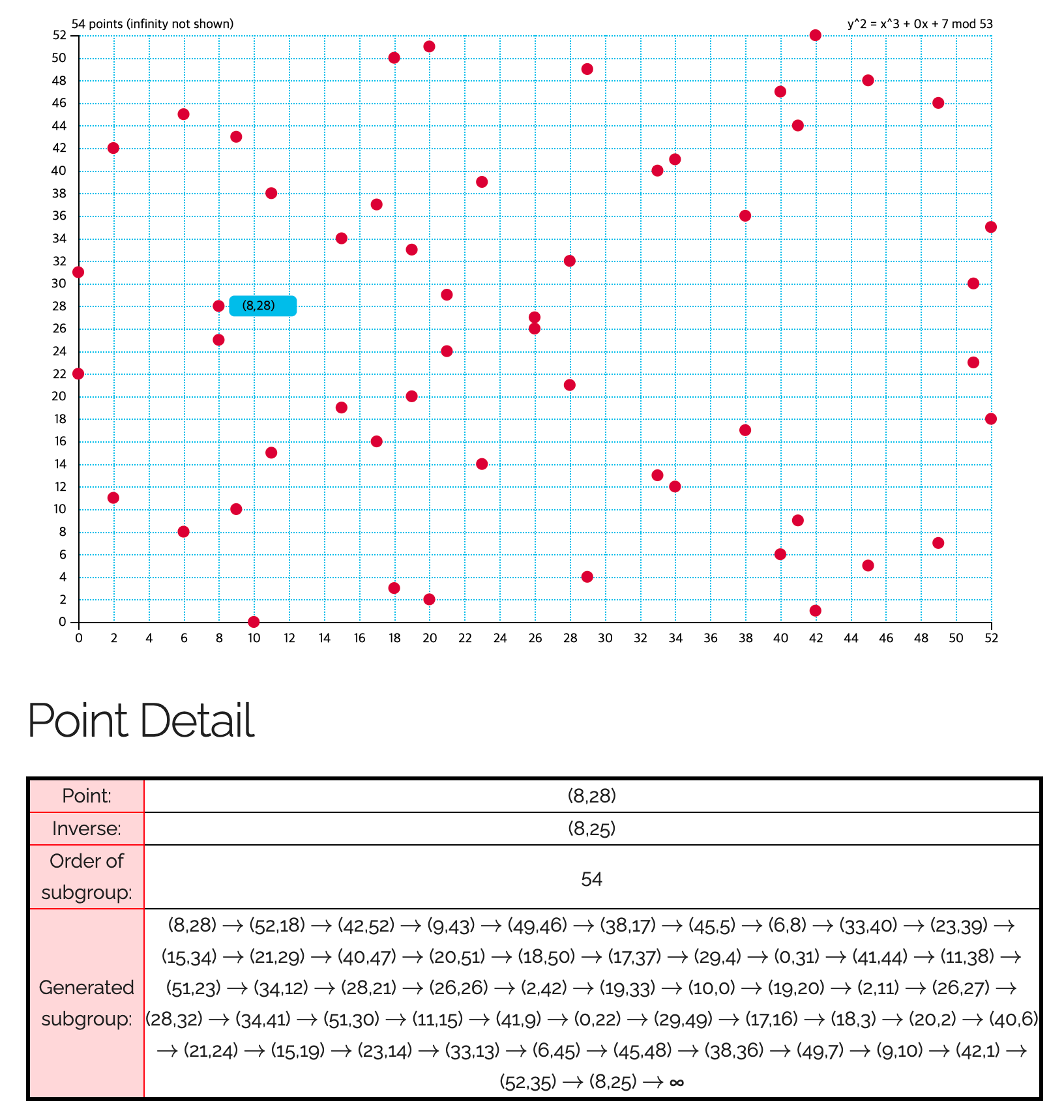
views
유한체의 타원곡선 위의 점

(8, 25) 의 inverse 가 (8, 23) 임을 알수 있다. y^2 에 따라 나타나는 성질로 이에 따라 y=(53/2)를 기준으로 상하 대칭이 되는 것을 확인할 수 있다.

곡선위에서의 덧셈 연산

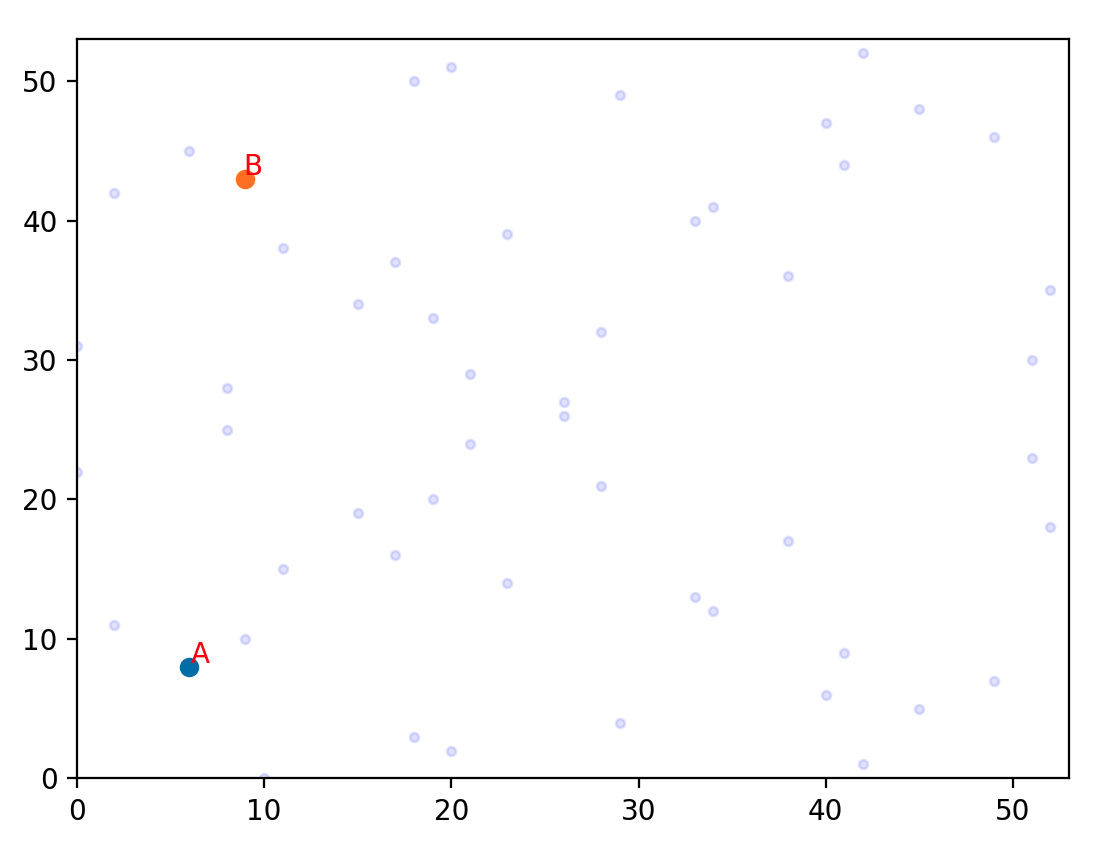
곡선 위의 두 점 A, B를 임의로 정하고, 곡선 위에 그려 보자.

A = Point(points[4][0], points[4][1], FieldElement(0, prime), FieldElement(7, prime))
B = Point(points[9][0], points[9][1], FieldElement(0, prime), FieldElement(7, prime))

plt.scatter(A.x.num, A.y.num)
plt.annotate('A', (A.x.num+0.1, A.y.num+0.25), c='r')

plt.scatter(B.x.num, B.y.num)
plt.annotate('B', (B.x.num-0.1, B.y.num+0.25), c='r')
views
유한체의 타원곡선 위의 두점

A와 B를 연결하는 직선을 찾자. modular 연산의 특징으로 y값이 53이 되면 다시 0부터 직선이 이어지는 특성을 갖는다.

# A와 B를 지나는 직선 찾기
la = (B.y.num - A.y.num) / (B.x.num - A.x.num)
lb = A.y.num - la*A.x.num

x_intercept = -(lb/la) 
x_distance =  (prime - lb) / la - x_intercept

# A+B 의 계산 
C = A+B

# A+B의 x축이 나올때 까지 직선 그려 보기
i = 0
while True:
    lx = np.linspace(A.x.num, C.x.num, 100)
    ly = (la * (lx - x_distance*i) + lb)
    plt.plot(lx, ly, linestyle='--', c='black', linewidth=1, alpha=0.5)
    if la * (C.x.num - x_distance*i) + lb == (prime - C.y.num):
        break
    i += 1
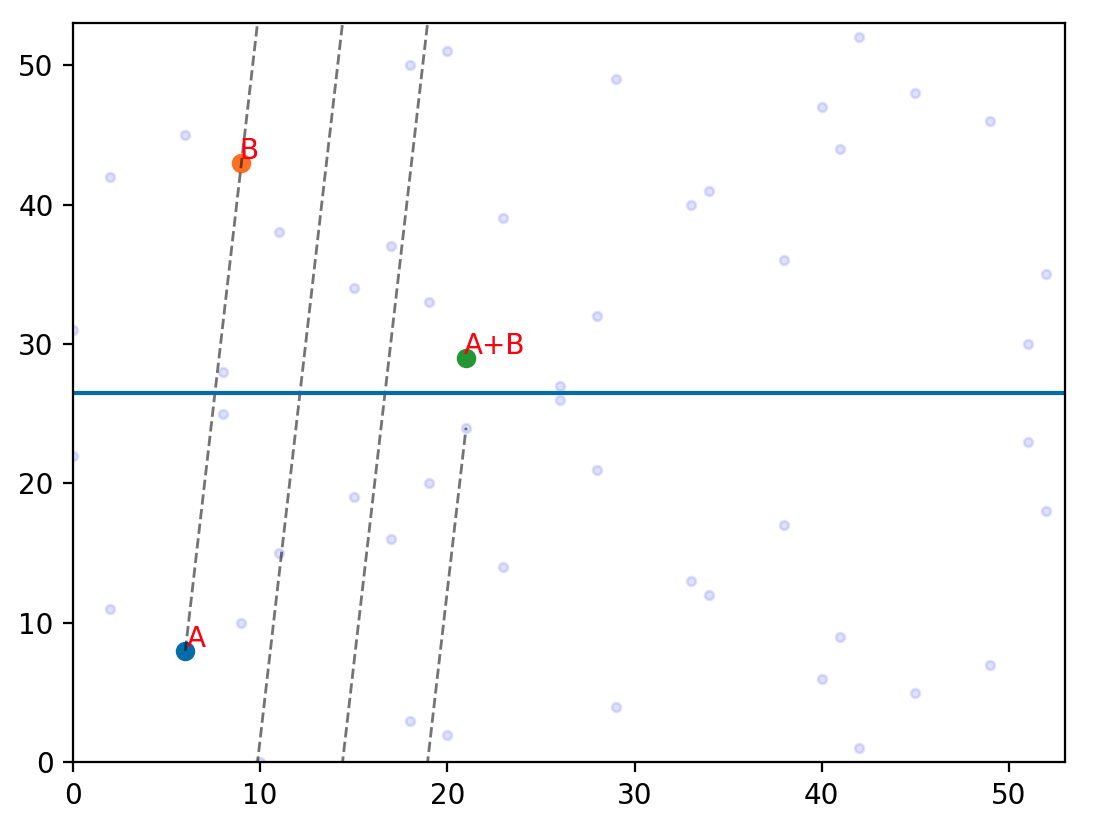
views
타원곡선 위의 두 점을 연결하는 직선

다시 한번 떠올려 보면, 타원 곡선의 덧셈은 다음과 같의 정의한다.

  • 두 점 A와 B를 지나가는 직선이 타원곡선과 새롭게 만나는 점 C를 찾는다.
  • 그 점과 X축에 대해 대칭인 점이 덧셈의 결과다.

유한체에서도 이어진 직선(비록 직선이 끝을 만나면 반대쪽에서 다시 이어지지만)이 유한체 내의 점을 찾게 되고, X축에 대해 대칭인 점이 덧셈의 결과가 된다.