회사 분들과 함께 Programming Bitcoin 책을 스터디하고 있다. 첫 3장에서 타원곡선 암호에 대해서 다루고 있는데, 이해가 부족한 느낌이 들어 다른 레퍼런스들을 찾아가며 다시 한번 구현 해 보고자 한다.타원 곡선

타원 곡선의 정의는 다음과 같다. 한번 그려보도록 하자. \(y^2 = x^3 + ax + b\)

import numpy as np
import matplotlib.pyplot as plt

# 타원 곡선을 정의하자. a와 b 는 곡선이 적당한 모양이 되도록 정했다.
def ec(x):
    return x**3 - 2*x + 2

fig, ax = plt.subplots(dpi=100)
# X, Y 축 모두 (-5, 5) 범위
y, x = np.ogrid[-5:5:100j, -5:5:100j]
# 가로, 세로선 표시
plt.grid()
# 등치선 그려보기
plt.contour(x.ravel(), y.ravel(), y**2 - ec(x), levels=[0])
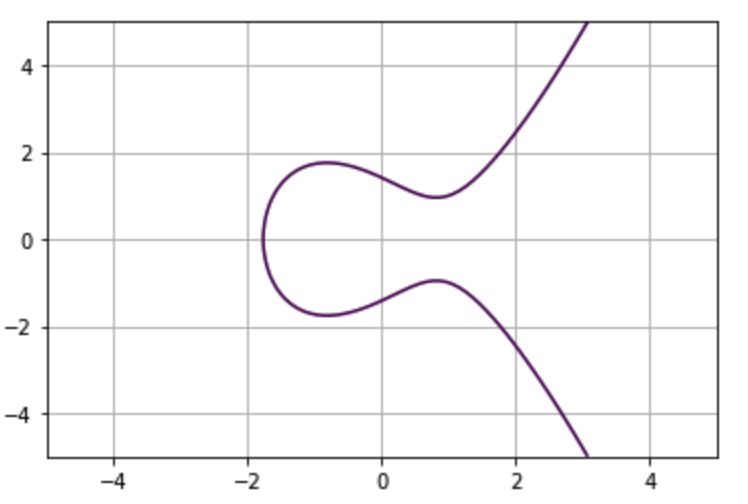
views
타원곡선

원래 생각하던 타원 모양은 아니다. 사실 타원 곡선의 “타원” 은 타원의 둘레를 구하기 위한 적분 계산에서 유래 되었다고 한다.

곡선위에서의 덧셈 연산

덧셈을 알아보기 전에 곡선위의 점을 정의해 보자.

class Point:
    def __init__(self, x, y=None):
        self.x = x
        if y is None:
            self.y = np.sqrt(ecc_r(x))
        
    def __repr__(self):
        return 'Point({}, {})'.format(self.x, self.y)

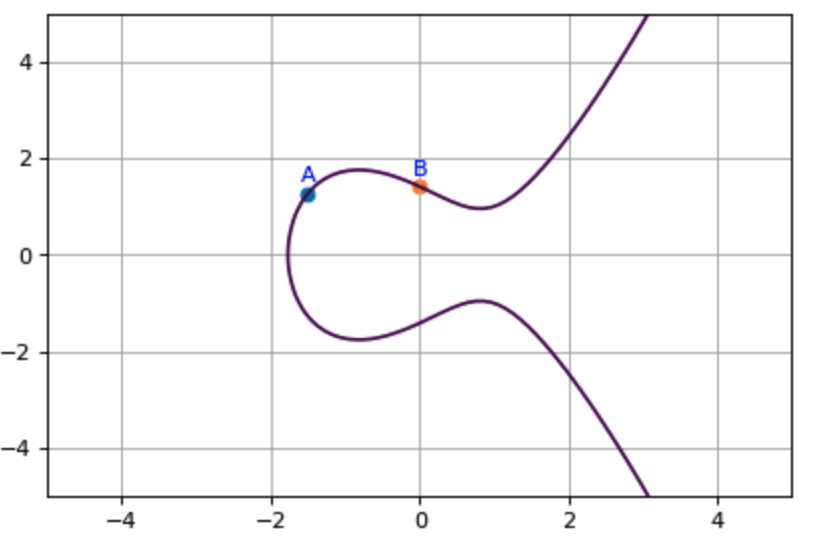
곡선 위의 두 점 A, B를 임의로 정하고, 곡선 위에 그려 보자.

# Point(-1.5, 1.2747548783981961)
A = Point(-1.5)
# Point(0, 1.4142135623730951))
B = Point(0)

ax.scatter(A.x, A.y)
ax.annotate('A', (A.x-0.1, A.y+0.25), c='b')
ax.scatter(B.x, B.y)
ax.annotate('B', (B.x-0.1, B.y+0.25), c='b')
fig
views
타원곡선 위의 두 점

타원 곡선의 덧셈은 다음과 같의 정의한다.

  • 두 점 A와 B를 지나가는 직선이 타원곡선과 새롭게 만나는 점 C를 찾는다.
  • 그 점과 X축에 대해 대칭인 점이 덧셈의 결과다.

곡선위에서의 덧셈은 두 점에 어떤 연산을 통해서 곡선위의 또 다른 점을 얻는것이다. 이 연산을 굳이 “덧셈” 이라고 하는 이유는 우리가 알고 있는 일반적인 덧셈의 속성들을 가지기 때문이다.

A와 B를 지나는 직선은 중학교 때를 떠올려 보자. 직선의 방정식은 \(y = ax + b\) 로 정의된다. 여기에서 기울기는 \(a = (y2 - y1) / (x2 - x1)\) 와 같이 구한다. y절편 b 는 x=0 일 때 식이다.

la = (B.y - A.y) / (B.x - A.x)
lx = np.linspace(-5, 5, 100)
lb = np.sqrt(ecc_r(0))
ly = la * lx + lb
ax.plot(lx, ly, linestyle='--', c='black', linewidth=1)
fig
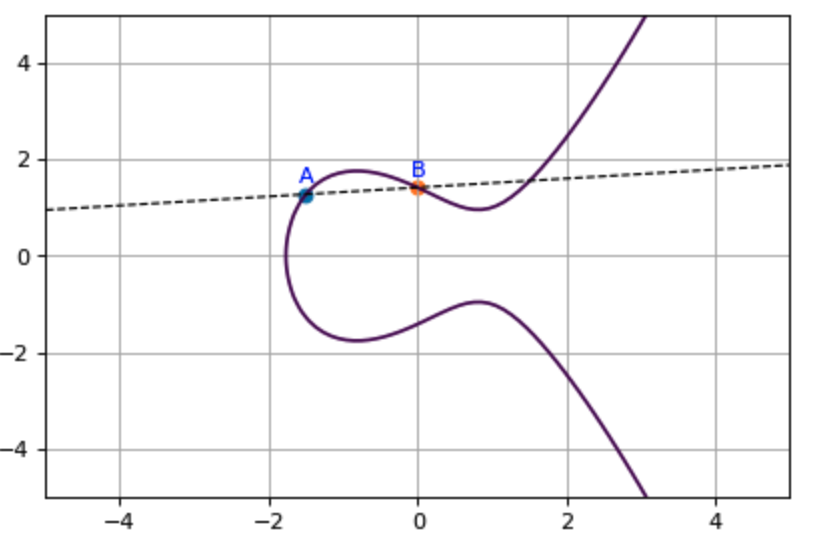
views
두 점 사이의 직선

타원 곡선 덧셈의 정의에 따라 직선과 타원 곡선이 만나는 점을 구하자. 선을 따라가며 근사값을 구해보도록 하자.

for x in np.linspace(0.2, 2, 100):
    ec_y = np.sqrt(ecc_r(x))
    line_y = lm * x + lb
    if np.isclose(ec_y, line_y, rtol=0.001):
        C = Point(x)
C
# Point(1.509090909090909,1.555170238373621)

적절한 값이 나온 것 같다. 교점과 X축에 대칭되는 점을 구해 보자.

ax.scatter(C.x, C.y)
ax.annotate('C', (C.x-0.1, C.y+0.25), c='b')

ax.scatter(C.x, -C.y)
ax.annotate('A+B', (C.x-0.1, -C.y+0.25), c='b')
fig
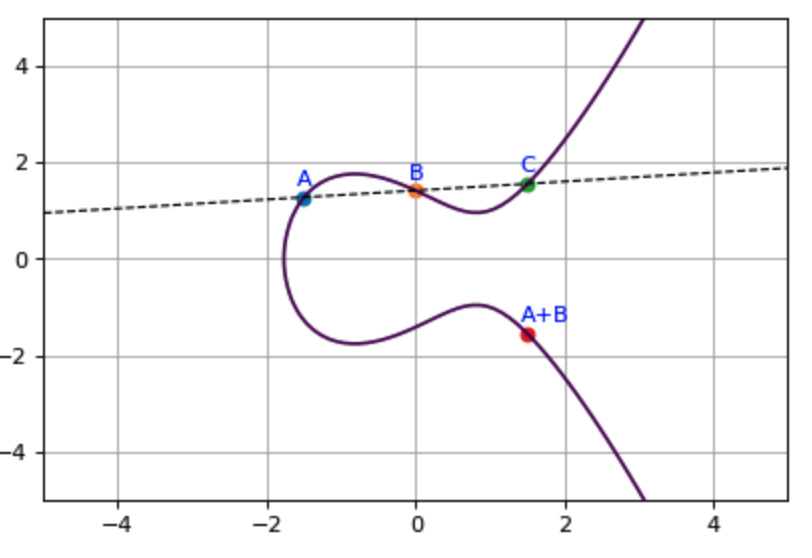
views
타원곡선의 덧셈

타원곡선의 덧셈을 구해 봤다. 다음번에는 유한체에서 정의된 타원곡선의 덧셈에 대해서 알아보고자 한다.